Here you will learn about lines of symmetry, including symmetry properties within polygons, angle properties, and symmetry of different line graphs.
Students first learn about line symmetry in grade 4 with their work with 2D shapes in geometry.
Lines of symmetry are straight lines that divide a shape into two equal parts, where one part is an exact reflection or mirror image of the other.
In geometry, many 2D shapes have line symmetry.
Line symmetry can be seen in nature.
Line symmetry can be seen in art.
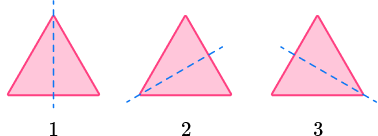
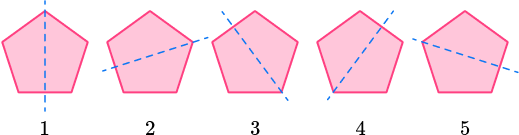
Regular polygons are polygons that have equal side lengths and equal angle measures.
Notice how each line of symmetry can be a fold line.
Notice how each line of symmetry can be a fold line.
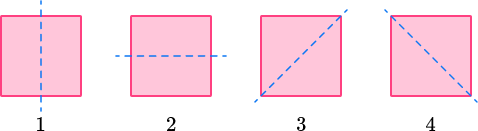
Notice how each line of symmetry can be a fold line.
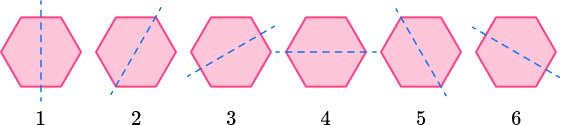
Notice how each line of symmetry can be a fold line.
Notice how the number of lines of symmetry in these regular polygons is equal to the number of sides and angles the polygons have.
All regular polygons share the property that the number of sides is equal to the number of lines of symmetry.
![[FREE] 2D Shape Worksheet (Grade 2 to 4)](https://thirdspacelearning.com/wp-content/uploads/2023/07/2D-shapes-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 2 – 4 students’ understanding of 2D shape. 10+ questions with answers covering a range of 2nd, 3rd and 4th grade 2D shape topics to identify areas of strength and support!
Use this quiz to check your grade 2 – 4 students’ understanding of 2D shape. 10+ questions with answers covering a range of 2nd, 3rd and 4th grade 2D shape topics to identify areas of strength and support!
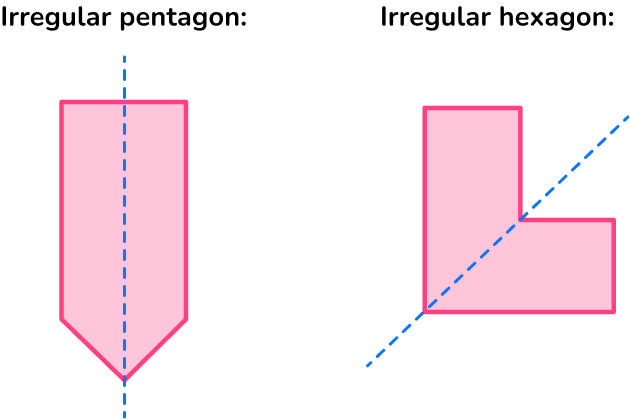
Irregular polygons are polygons that do not have all equal angles and all equal side lengths. However, they can have line symmetry.
For example, these irregular polygons have line symmetry.
Let’s look at different shapes (specifically quadrilaterals) and their number of lines of symmetry.
| Quadrilateral | Image | Number of Lines of Symmetry |
|---|---|---|
| Square | 4 | |
| Rectangle |  | 2 |
| Parallelogram |  | 0 |
| Rhombus | 2 | |
| Kite |  | 1 |
| Trapezoid | 0 | |
| Isosceles Trapezoid |  table image 13" width="169" height="82" /> | 1 |
| Irregular | 0 |
The diameter of a circle splits the circle into two equal sized half circles, or semicircles. Think of the diameter as the line of reflection.
A circle can be folded in-half many ways, meaning that there are an infinite number of lines of symmetry.
