

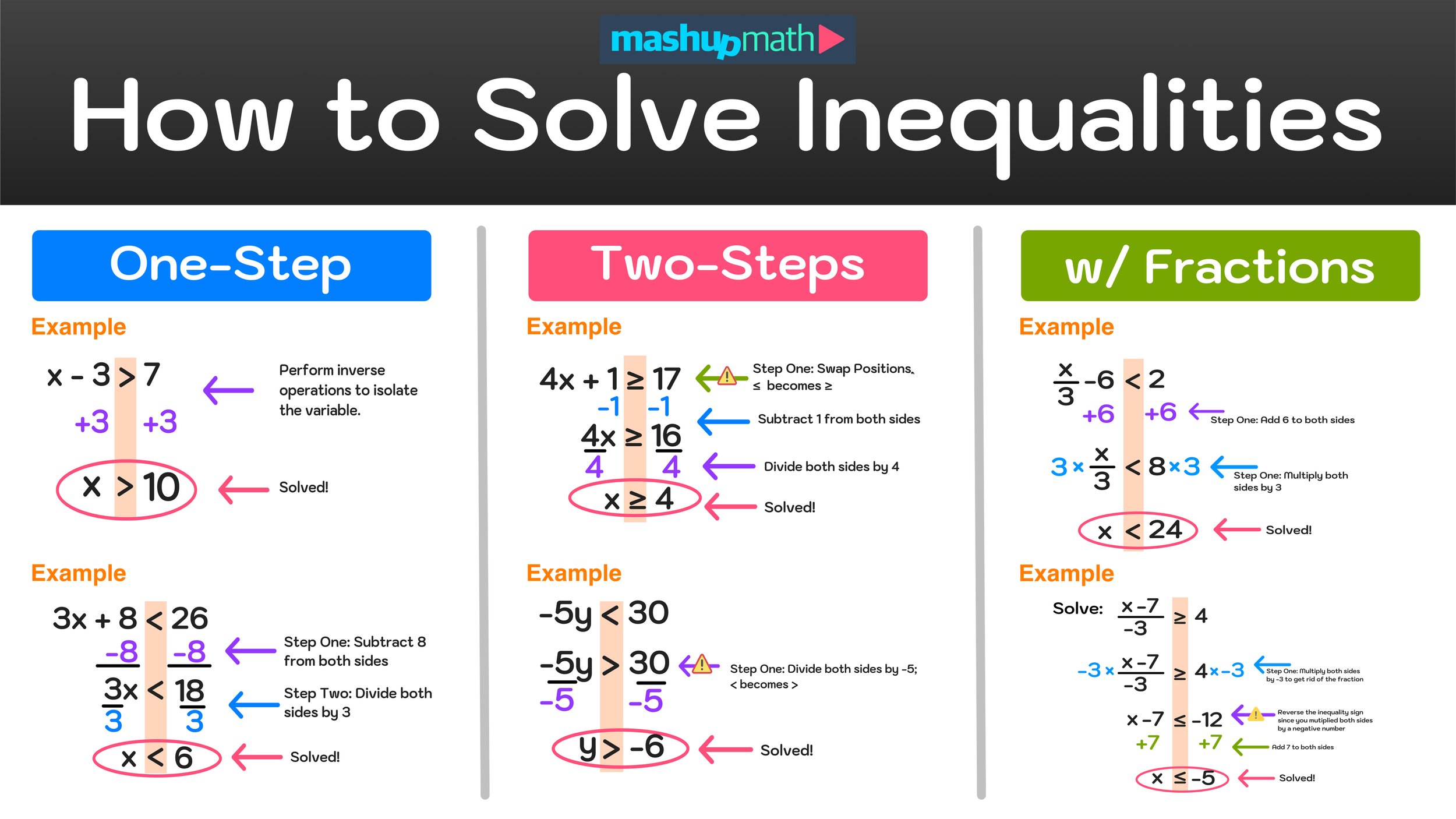
In math, an inequality is a symbol that is used to represent the relationship between two values or expressions that are not necessarily equal to each other. There are four types of inequality symbols:
Understanding how to solve inequalities is an important math skill that all students will need to be successful in algebra and beyond. To acquire this skill, you will have to build upon your knowledge of solving equations and extend that understanding to solving inequalities.
This free Step-by-Step Guide on How to Solve Inequalities covers the following:
While learning how to solve an inequality is a little trickier than learning how to solve an equation, you can easily learn how to solve inequalities by working through this guide. By working through the step-by-step practice problems below, you will gain plenty of helpful practice with solving inequalities, which will put you on the path of being able to solve any inequality with ease.
While you are probably eager to dive into a few practice problems, let’s start off with a quick review of a few key vocabulary terms that you should deeply understand before you begin learning how to solve an inequality.
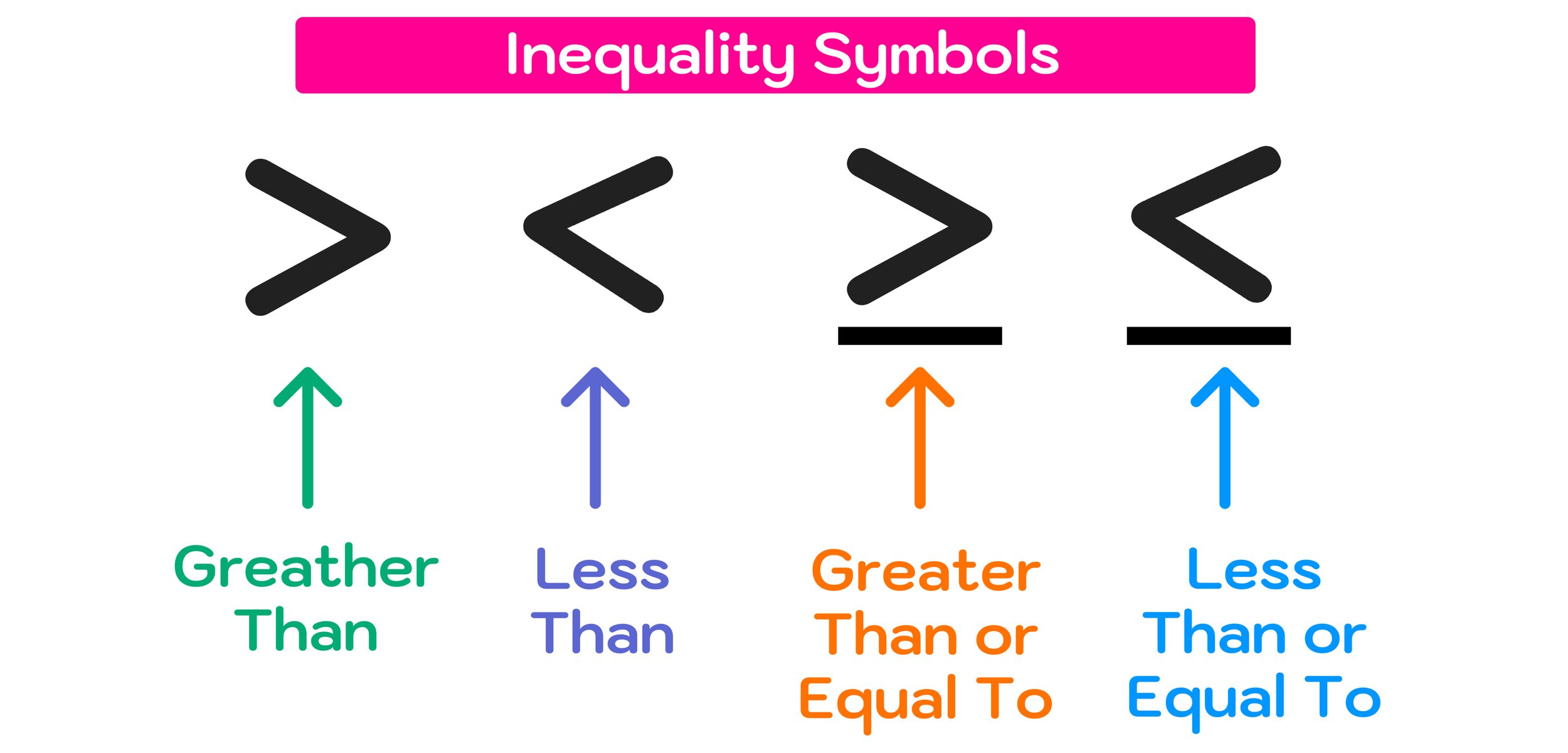
As said earlier, in math, an inequality is a relationship between two values or expressions that are not equal to each other. Because the values or expressions are not equal to each other, we have to use an inequality sign instead of an equals (=) sign.
Basic inequalities do not need to be solved since the variable is already by itself.
For example, consider the inequalities x>7 and y≤-3.
These inequalities can be thought of as solved because the variables are already on their own. These “solved” inequalities are illustrated in Figure 02 below.
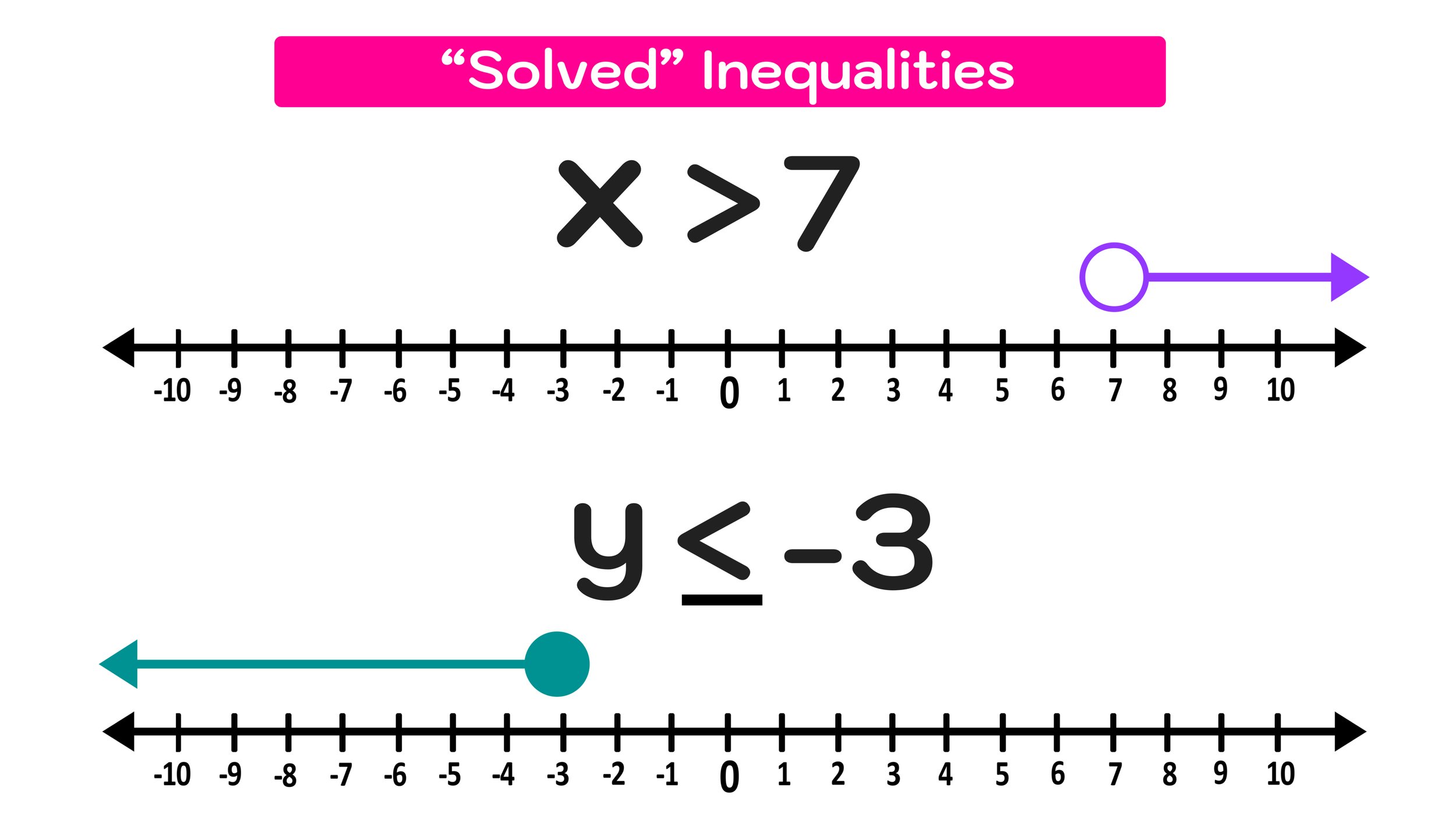
But, what if we had an inequality that looked like this: x - 3 > 7
Since the variable, x, is not by itself, this inequality still needs to be solved, and the remainder of this guide will show you exactly how to do that.
Now that you are familiar with the key vocabulary terms, it’s time to look at a few examples.
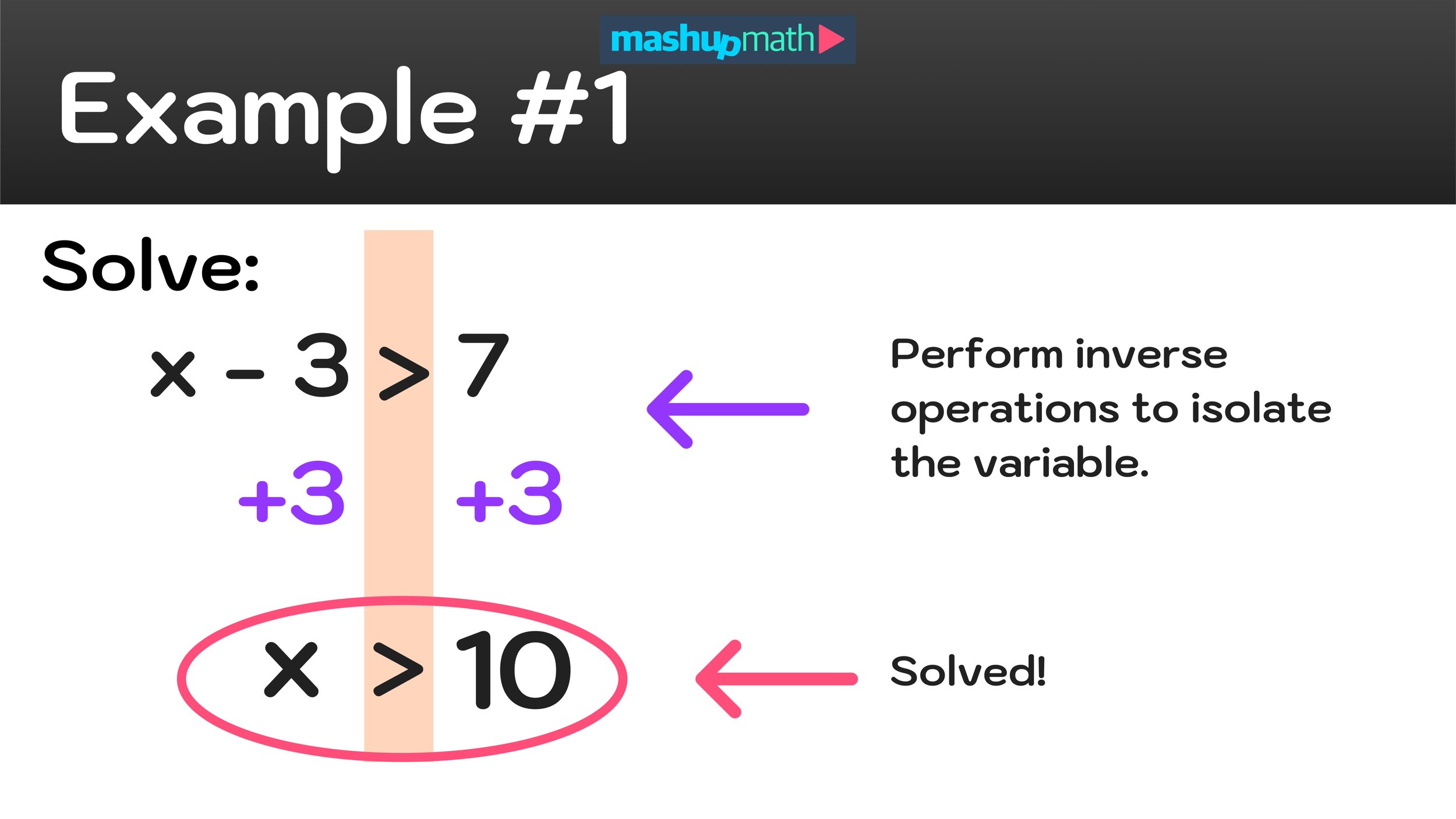
Example: x - 3 > 7
Just as you would solve an equation, to solve an inequality, you must use inverse operations to isolate the variable, which, in this example, is x.
You can isolate x easily by adding 3 to both sides of the inequality sign as follows:
Now the inequality is solved! The answer is x>10. The step-by-step procedure to solving this first example is illustrated in Figure 03 below.
This first example of how to solve inequalities was relatively simple and only took one step to solve. Now, let’s move onto solving a slightly more difficult inequality.
Example: 3x + 8 < 26
Again, to solve the inequality you have to isolate the variable x by performing inverse operations as follows:
Solving this example required two steps (step one: subtract 8 from both sides; step two: divide both sides by 3). The result is the solved inequality x
The step-by-step procedure to solving example #2 is illustrated in Figure 04 below.