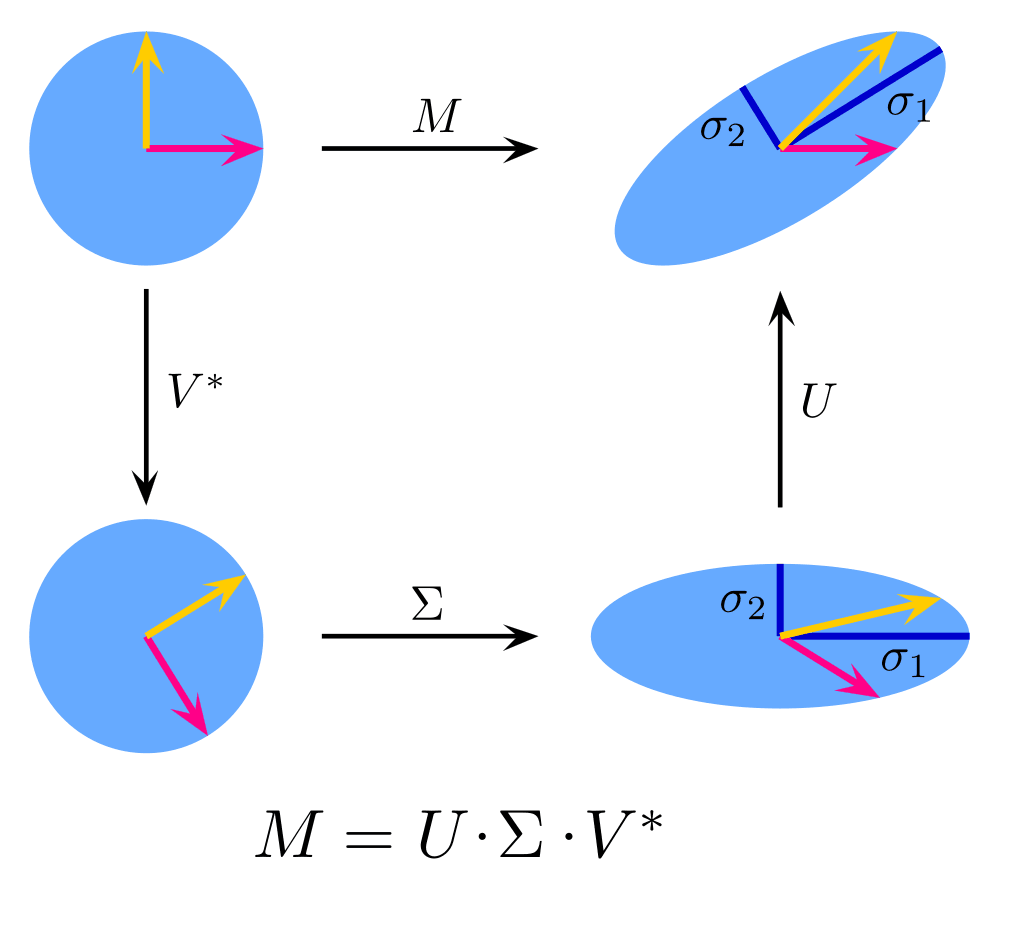
Truncated SVD is a popular technique in machine learning for reducing the dimensions of high-dimensional data while retaining most of the original information. This technique is particularly useful in scenarios where the data has a large number of features, making it difficult to perform efficient computations or visualize the data.
Truncated SVD works by decomposing a matrix into its singular values and vectors and then selecting only the top k singular values and vectors, where k is a user-defined parameter.
This results in a reduced matrix that captures most of the original information while significantly reducing the number of dimensions. One of the advantages of truncated SVD is that it can be used with both sparse and dense matrices, making it a versatile technique for various machine learning applications.
In addition, truncated SVD can help reduce the impact of noise or redundancy in the data, which can improve the accuracy of machine learning models.
However, it's important to note that truncated SVD also has some limitations. For instance, it may not work well with data that has complex relationships between its features.
In this beginner's guide, we will explore the advantages and limitations of truncated SVD in detail.
Ultimate Guide For Using Truncated SVD For Dimensionality Reduction
Click to TweetWe will also discuss how truncated SVD can be used in practical machine learning workflows, including how to choose the optimal number of dimensions and how to interpret the results.
Moreover, we will provide a step-by-step guide to implementing truncated SVD using popular Python libraries like NumPy and Scikit-learn.
By the end of this article, you should have a solid understanding of truncated SVD and how it can be used to reduce the dimensions of high-dimensional data in machine learning.
Whether you're new to machine learning or a seasoned data scientist, this guide will equip you with the knowledge and skills to apply truncated SVD to your machine learning projects.
Table of ContentsIn today's data-driven world, it's important to have the tools and technology to manage the huge amount of data that has been created. Singular value decomposition (SVD) and truncated SVD are powerful mathematical techniques used in data analysis and machine learning to reduce residual data and improve the accuracy of machine learning models.
The image reference taken from Wikipedia
Singular Value Decomposition (SVD) is a matrix decomposition method that decomposes a matrix into three matrices: U, Σ, and V. In SVD, the matrix U represents left-hand side vectors, Σ represents positive values, and V denotes the right word. vectors. vector.
SVD is a popular data analysis and machine learning technique because it can be used to reduce residual data while retaining the most important data.
SVD has many applications, including image compression, natural language processing, and recommender systems. SVD allows you to transform a high-dimensional data set into a low-dimensional space that contains the most important information.
Truncated Singular Value Decomposition (SVD), an insightful dimensionality reduction technique, emerges as a pivotal player in the arena of data analysis, particularly in scenarios suffused with high-dimensional datasets.
It operates by pinpointing and preserving only the top k singular values, along with their corresponding singular vectors, facilitating a reduced, yet informationally rich, representation of the original data.
As a less computationally demanding variant of SVD, Truncated SVD gracefully navigates through the ocean of data, offering a blend of computational efficiency and information retention.
Embedded in its framework is the capability to carve out a suboptimal solution, an approximation, by focusing on dominant singular values and vectors, thus encapsulating the majority of the data's variance and essential characteristics within a lower-dimensional space.
This aspect makes it especially valuable when we are sailing through the waters of large-scale data, where computational resources might be stringent and optimality needs to be balanced with efficiency.
In the realm of machine learning and data mining, Truncated SVD manifests its utility in numerous applications. It operates as a powerful tool to sieve through the redundancy and noise embedded in the data, honing in on the salient features that are crucial for predictive modeling.
By reducing the dimensionality of the dataset while maintaining its substantive informational content, it facilitates models to learn efficiently and effectively, minimizing the risk of overfitting, especially in scenarios characterized by a disparity where the feature space significantly outstrips the number of observations.
Moreover, Truncated SVD finds its applicability stretching across various domains, including natural language processing (NLP), where it is employed in Latent Semantic Analysis (LSA) to discern the underlying semantic structure in textual data by reducing the dimensionality of term-document matrices.
In collaborative filtering, it assists in approximating user-item interaction matrices, thereby aiding in crafting personalized recommendations. Furthermore, in the domain of image processing, it empowers the compression and noise reduction of image data, enabling the efficient storage and processing of visual information.
In addition to its capability to enhance model accuracy and learning, Truncated SVD enhances interpretability by transforming the data into a lower-dimensional space where the relationships between variables can be more readily discerned.
This particularly finds relevance in exploratory data analysis, where deciphering the underlying patterns and structures within the data is pivotal.
Truncated Singular Value Decomposition (Truncated SVD) has become a popular tool for reducing the dimensions (or simplifying) our data while keeping its important information.
But how does it manage to do this?
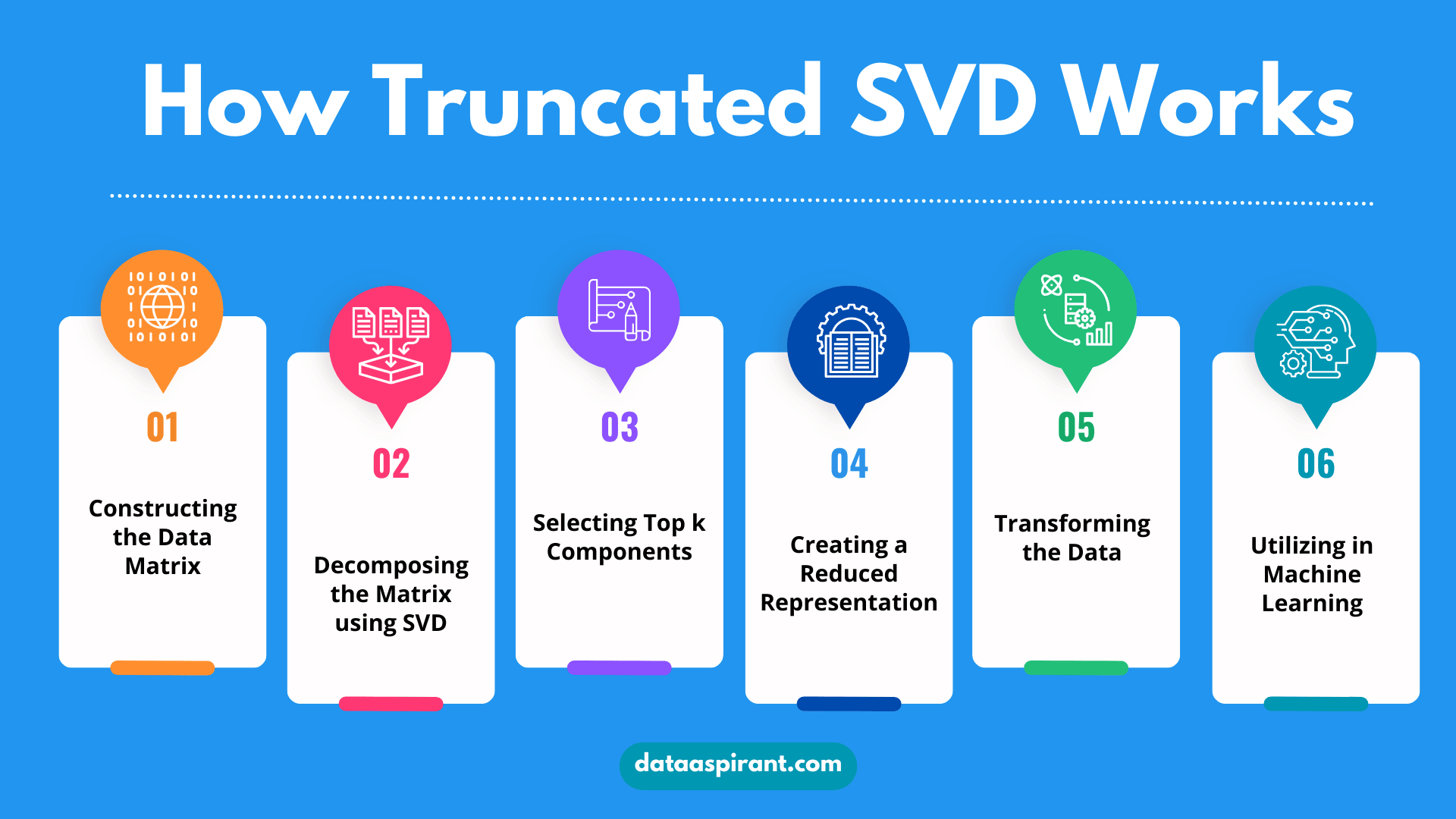
Let's embark on a journey through the step-by-step process of how Truncated SVD works, breaking it down into digestible chunks.
The first step involves organizing our data into a matrix. Imagine we have a dataset of book reviews, where each word is a feature, and each review is an observation. We create a matrix where each row represents a review and each column represents a word.
The entries of this matrix might represent the frequency of words in each review.
Next, the SVD method breaks down our original matrix (let’s call it (A)) into three separate components: