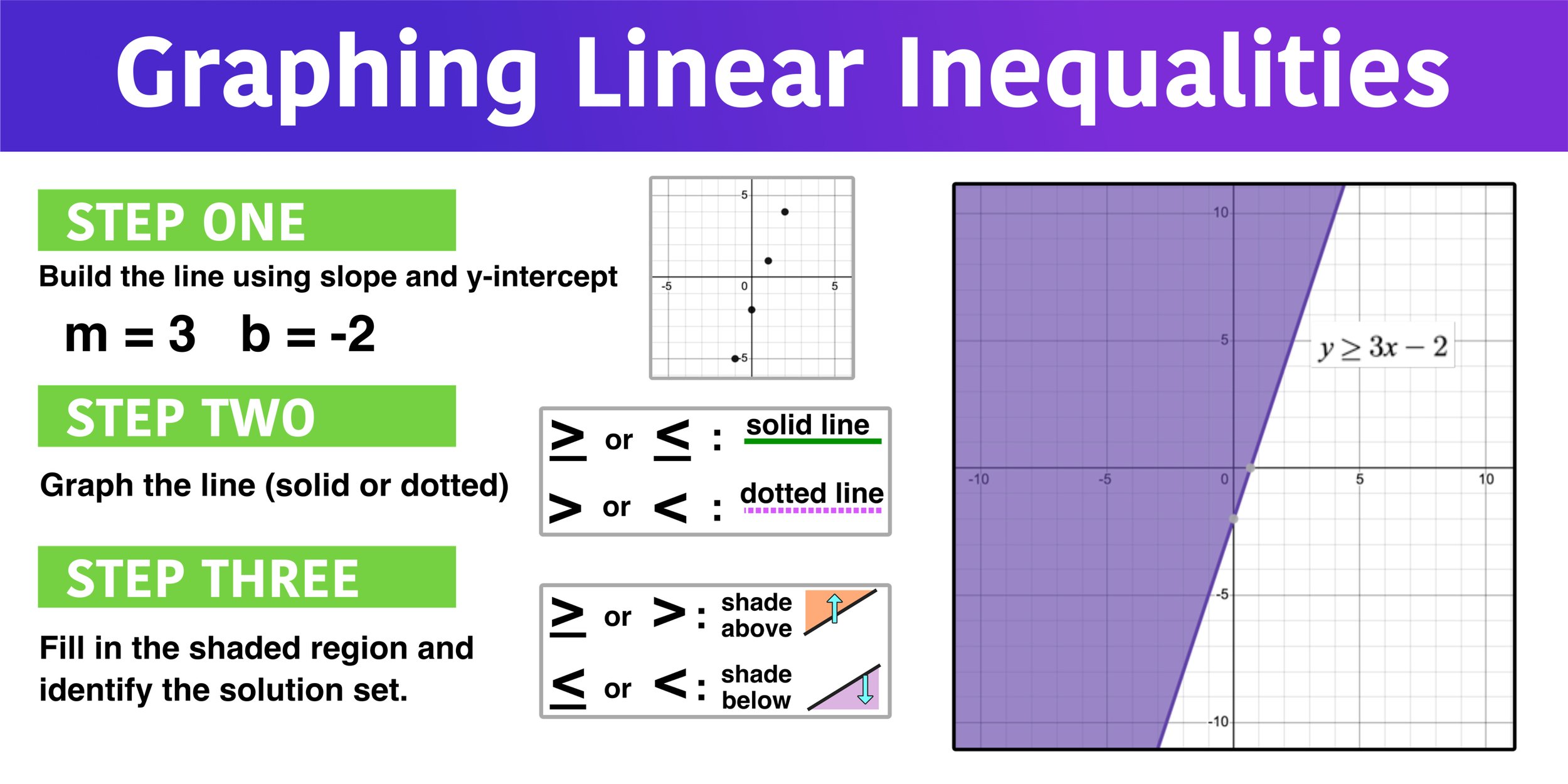


Welcome to this simple and straightforward guide to graphing linear inequalities on the coordinate plane. By the end of this guide, you will be able to:
By working through three examples, you will gain experience and understanding of both of these skills.
However, before going forward, make sure that you are familiar with graphing linear equations in y=mx+b form where m represents the slope and b represents the y-intercept.
Graphing linear inequalities is similar to graphing linear equations (with a few extra steps) and this pre-requisite knowledge is required. If you need a recap of graphing lines in y=mx+b form, we suggest that you review our free Graphing Lines Using Slope step-by-step guide for students.
Once you are able to graph a linear equation in y=mx+b form, you are ready to start graphing linear inequalities in y>mx+ b (or y
But first, let’s quickly review some important math concepts and definitions related to linear relationships and inequalities that will help you along the way.
Let’s start by considering the equation x+5=8. Using simple algebra, you can figure out that the solution to this equation is x=3 (see Figure 01).

For this equation, 3 is the only possible solution that would make the equation true and all other values would not work (we can these values non-solutions).
Key Takeaway: Equations can have only one possible solution.
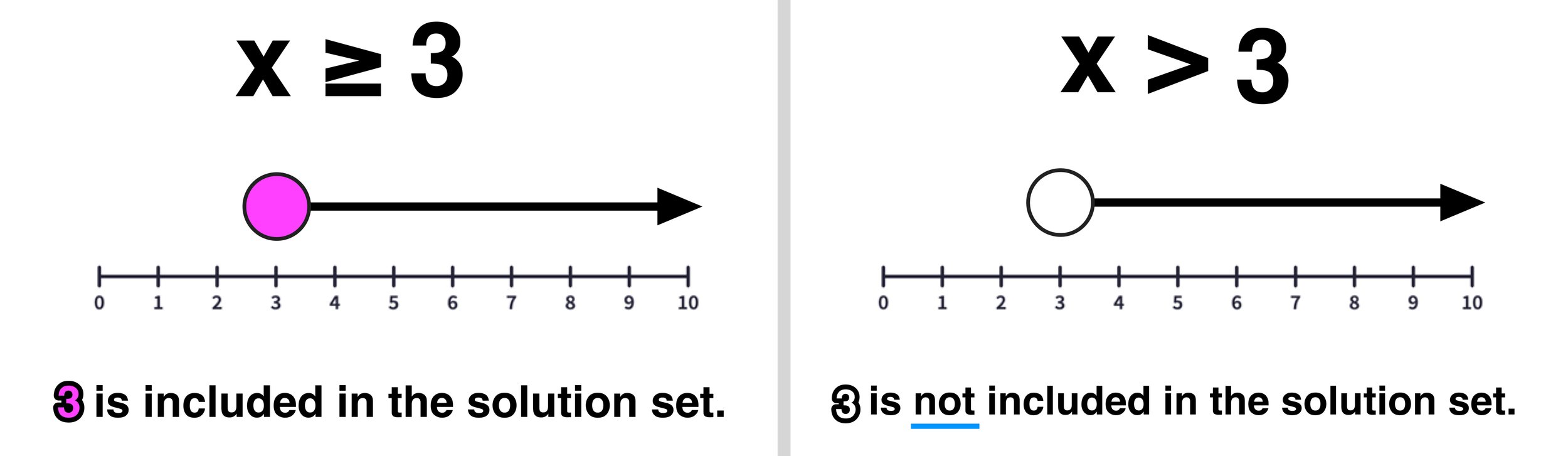
What if we change the equation x+5=8 to the inequality x+5≥8? Using algebra, you can conclude that the solution to the inequality is x≥3.
The solution x≥3 means the value 3 and any value greater than 3 is a possible solution. And there are an infinite amount of values that satisfy this criteria. This infinite set of values that could be solutions to an inequality is called the solution set .
Additionally, if we change the inequality from ≥ to > as follows: x+5>8, you can conclude that the solution to the inequality is x>3.
The solution x>3 means that any value greater than 3 is a possible solution, but not including 3.
You can visualize the solutions to x+5≥8 and x+5>8 on the number line as shown in Figure 02 (the distinction between the solutions of ≥/≤ and >/< inequalities is important to understand before moving forward).
Key Takeaway: Inequalities can have an infinite amount of possible solutions.
Next, we can ask what do linear inequalities and their solution sets look like on the coordinate plane?
Let’s again start with your understanding of linear equations and then building upon it to help you to understand linear inequalities.
For example, consider the linear equations
Both of these linear equations are in y=-mx+b form where m represents the slope and b represents the y-intercept. The first equation has a slope of positive 2 and y-intercept at 1 and the second equation has a slope of negative 2 and y-intercept at 1.
Figure 03 below shows what the graphs of these linear equations looks like:

Next, let’s change both equations to inequalities as follows:
These linear inequalities are in y≥mx+b and y≤mx+b form. In fact, they are very similar to their equation counterparts in that the first inequality has a slope of positive 2 and y-intercept at 1 and the second inequality has a slope of negative 2 and y-intercept at 1.
Figure 04 below shows what graphing these linear inequalities looks like:

Notice that the graphs of the equations and the graphs of the inequalities have the same lines, but that the inequality includes shaded region.
Why? When you graph a linear equation, all of the points on the line are solutions to the equation, while all of the points that are not on the line are non-solutions. When you graph a linear inequality, points on the line can be solutions (more on this later) as well as all of the points in the shaded region, which is called the solution set.
At this point, it should also be noted that, just like inequalities on the number line graphs, there is a difference between the solution sets of ≥/≤ and >/< inequalities. Namely, that the solution set of ≥/≤ inequalities includes points on the line, while >/< inequalities do not include points on the line.
Are you confused? That’s okay. Let’s take a deeper look at the difference between solid and dotted lines as well as when to shade above or shade below an inequality.
Solid Lines vs. Dotted Lines:
Example: Figure 05 below compares the linear inequalities y>x+1 and y≥x+1. Notice that both inequalities have a shaded region and that y>x+1 has a dotted line, while y≥x+1 has a solid line.